Persamaan Euler adalah persamaan diferensial. Dengan mengintegrasikan sepanjang garis arus, praktis persamaan euler dapat diturunkan menjadi persamaan yang dikenal sebagai persamaan Bernoulli. Persamaan Bernoulli diperoleh dengan mengintegrasikan persamaan Euler (persamaan (3.48)):
Jika diasumsikan bahwa densitasnya konstan (yaitu fluida tidak dapat dimampatkan), maka
Persamaan diatas adalah persamaan Bernoulli, dan itu hanya berlaku untuk situasi berikut:
● aliran tidak kental;
● aliran tak mampu mampat; (aliran tidak kental dan tak mampu mampat dikenal sbg aliran ideal)
● aliran steady (stabil);
● kerja poros nol;
● mengalir di sepanjang garis arus.
Setiap suku dalam persamaan Bernoulli memiliki satuan energi, dan persamaannya adalah pernyataan khusus dari hukum kekekalan energi yang berlaku untuk aliran ideal di mana: tidak ada kerugian gesekan atau transfer energi seperti kerja yang terjadi. Tiga suku dalam persamaan tersebut berhubungan erat dengan tiga jenis energi yang berbeda dimana fluida memiliki
● Suku pertama
P/ρ merupakan energi yang dibutuhkan untuk memindahkan cairan melawan tekanan lokal dalam cairan. Istilah ini kadang-kadang dikenal sebagai kerja aliran atau energi aliran.
● Suku kedua
gz adalah suku elevasi dan berhubungan dengan energi yang dibutuhkan untuk menaikkan fluida
melawan gravitasi. Ini adalah istilah energi potensial.
● Suku ketiga
v2/2 berhubungan dengan kecepatan, dan karenanya mewakili energi kinetik dalam fluida.
Persamaan Bernoulli secara sederhana menyatakan bahwa energi dalam fluida karena tekanan, elevasi dan gerak dikonservasikan (baca: kekal/konstan) asalkan tidak ada input energi eksternal dari pompa atau kipas (tidak ada kerja poros) dan tidak ada viskositas yang menghilangkan energi kinetik sebagai panas. Hal ini mirip dengan konsep yang mengasumsikan gerak tanpa gesekan dalam mekanika, dimana gesekan antara dua permukaan menimbulkan panas. Persamaan Bernoulli juga dapat disusun ulang menjadi bentuk yang sedikit berbeda, seperti yang ditunjukkan di bawah ini
Bentuk Head dari Persamaan Bernoulli
Jika setiap suku dalam persamaan Bernoulli dibagi dengan g, maka setiap suku memiliki satuan panjang (elevasi) dan disebut head . Head mewakili bobot energi. Bentuk Head persamaan Bernoulli adalah
Penggunaan istilah head dalam mekanika fluida sangat umum. Tiga suku dalam Persamaan Bernoulli disebut sebagai
Jumlah dari ketiga Head disebut sebagai head total, HT. Dengan demikian
Hp + z + Hv = HT
Ht adalah konstan, dan antara dua lokasi, 1 dan 2, tidak ada perubahan head total:
HT1 = HT2
Besaran (Hp + z) disebut head piezometrik, HPZ, dan p + gz adalah tekanan piezometric. Head piezometrik tidak memiliki arti khusus dan hanya kombinasi yang pas.
Bentuk Tekanan dari Persamaan Bernoulli
Jika setiap suku dalam persamaan Bernoulli dikalikan dengan , maka setiap suku memiliki satuan tekanan. Bentuk tekanan dari persamaan Bernoulli adalah
Tiga suku dalam persamaan bernoulli disebut sebagai
Jumlah dari ketiga tekanan disebut sebagai tekanan total PT. Maka,
PT konstan, dan antara dua lokasi, 1 dan 2, tidak ada perubahan pada head tekanan total:
PT1 = PT2
Besaran P + ρgz disebut dengan tekanan piezometrik


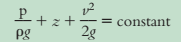
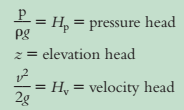


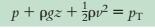
Tidak ada komentar:
Posting Komentar